Période : 2014 – 2015
Membres impliqués : Marc Daniel, Gilles Gouaty, Romain Raffin.
Collaborations : équipe INSM LSIS, équipe Image LE2I, financement Instituts Carnot STAR ET ARTS.
Mots-clés : Modélisation déclarative, Contraintes géométriques, Surfaces paramétriques, Surfaces de subdivision, Solveurs de contraintes.
Description du projet :
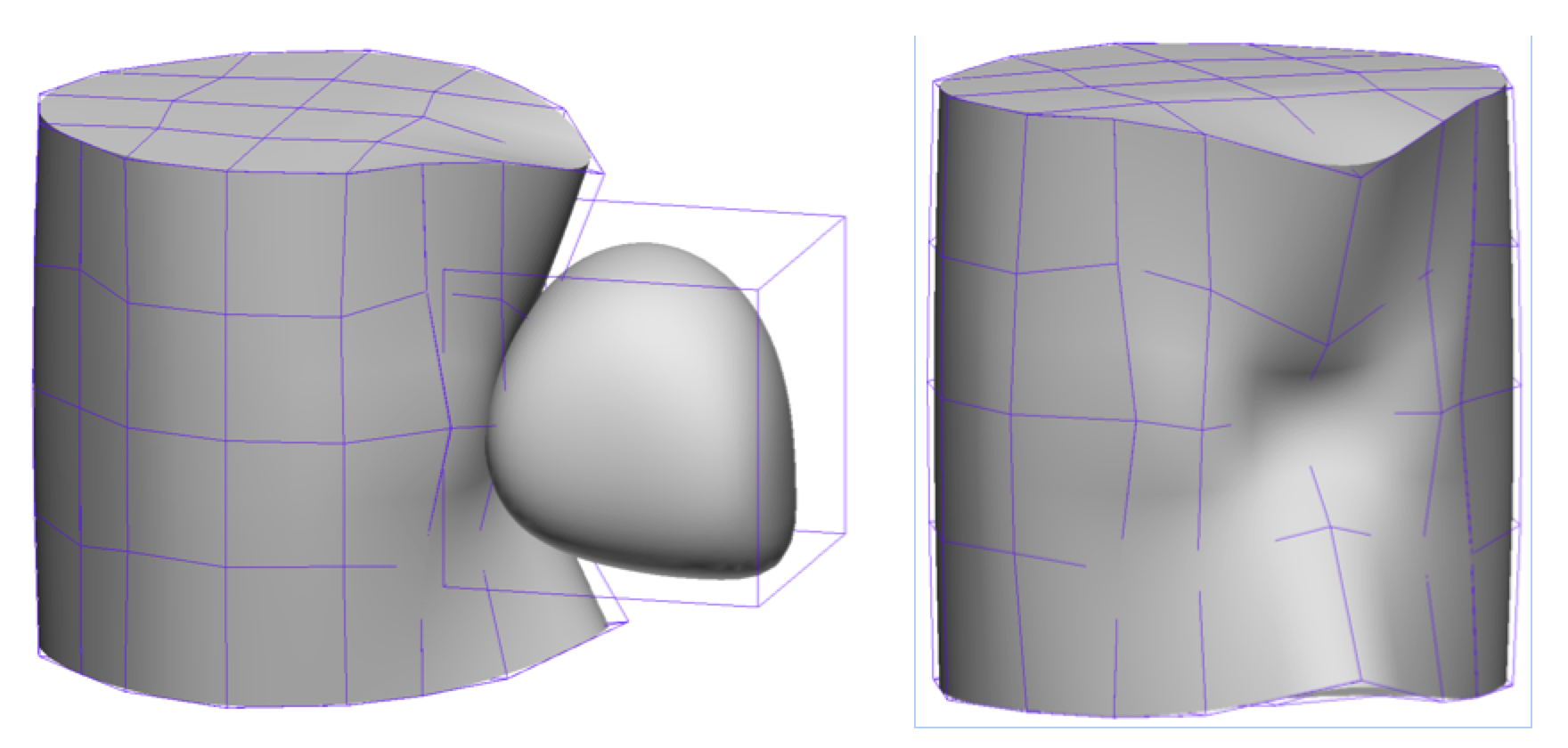
La modélisation géométrique a atteint une maturité au niveau des outils mathématiques permettant de créer les modèles à partir de surfaces dites à pôles (Bézier, B-splines, NURBS). Les manques sont essentiellement sur des méthodes de plus haut niveau permettant de concevoir les objets en termes de propriétés et/ou de contraintes correspondant aux métiers auxquels les objets s’adressent. Par ailleurs, le modèle mathématique s’appuyant sur les surfaces de subdivision a totalement envahi le monde de l’animation et du cinéma (films d’animation). Il n’est par contre pas entré dans celui de la Conception Assistée par Ordinateur (CAO). Or les complémentarités avec les surfaces à pôles sont fortes. Concevoir des modèles de subdivision à partir de contraintes est aussi un défi nouveau. Envisager de mêler dans cette même approche les surfaces à pôles et les surfaces de subdivision est totalement nouveau et permettrait d’avoir des modèles d’objet tirant parti des deux modèles mathématiques sous-jacents. C’est l’objectif de ce projet en finalisation. Les contraintes géométriques sont exprimées sous forme d’un langage qui sont ensuite traduites en fonctions mathématiques qu’un solveur résoudra.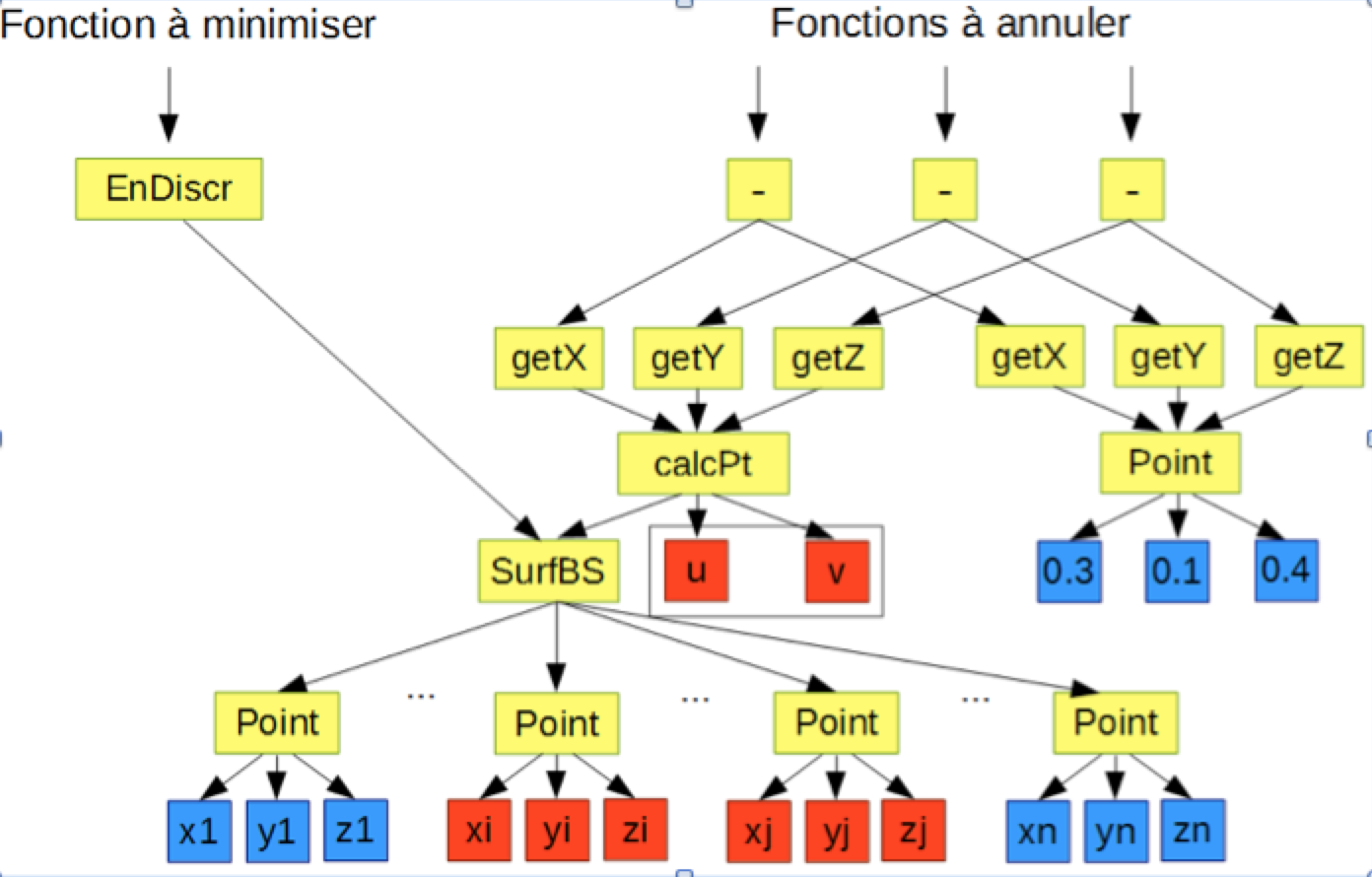

Commentaires récents