Introduction

L’équipe G-Mod, membre du laboratoire LIS UMR 7020, a été créé pour mettre en valeur la recherche en modélisation géométrique. G-Mod a au cœur de ses préoccupations la modélisation géométrique, qu’elle soit continue ou discrète.

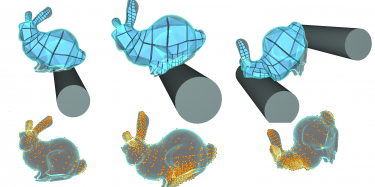
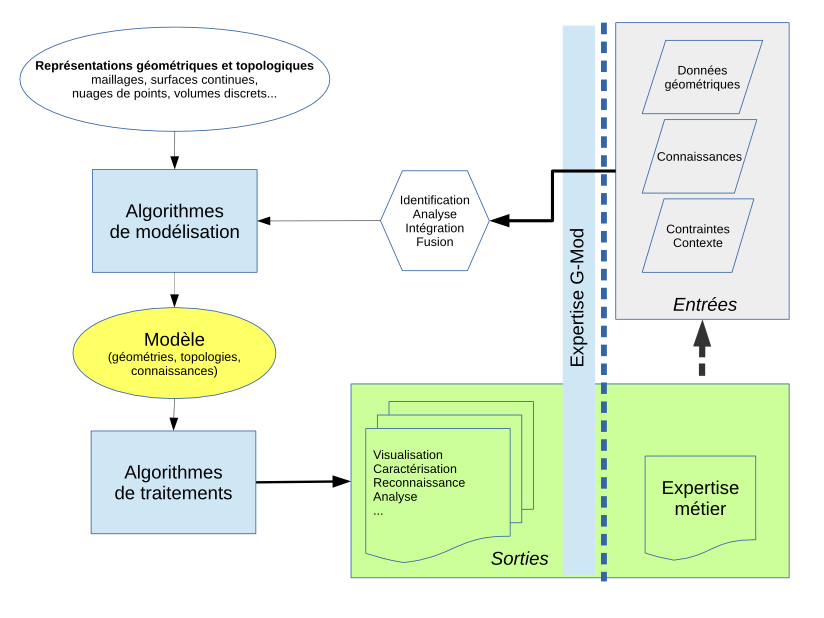Dans le domaine continu, nous nous intéressons essentiellement à la modélisation surfacique paramétrique à travers les modèles classiques B-splines ou NURBS, ainsi qu’aux fonctions implicites. Dans le domaine discret, nos travaux sont essentiellement centrés sur les maillages surfaciques. Au niveau des maillages de nombreux traitements sont nécessaires : simplification (maillages trop denses), amélioration (en particulier pour améliorer les zones sous-échantillonnées), et analyse de formes, que ce soit en tout point du maillage ou pour la détection de lignes caractéristiques (crêtes, ravins, failles), de zones homogènes. Les sources de données sont de plus en plus variées. Prendre en compte et fusionner ces données est aujourd’hui déterminant. La connaissance que l’on peut extraire des données ou la connaissance introduite pour construire les modèles prennent une place de plus en plus importante dans nos activités de recherche. La complexité des problèmes et de leurs données conduisent aux notions de multi-échelles et multi-modèles et des passages entre toutes ces représentations.

Les algorithmes que nous développons doivent être adaptés aux différents domaines d’applications :
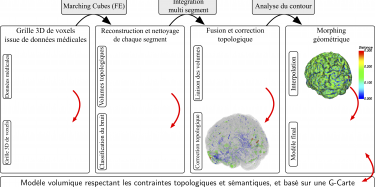
Utilisation du modèle géométrique dans les applications de type SIG (Système d’Information Géographique) par exemple pour la modélisation de réseaux réalistes de routes – Reconstruction d’organes dans le cadre d’applications médicales – Modélisation géométrique et sémantique associée au patrimoine archéologique – Analyse et modélisation de peuplements forestiers à partir de données LiDAR terrestre – Analyse topologique fine (via l’homologie) appliquée à la caractérisation de volumes binaires 3D (détection de l’ostéoporose, caractérisation d’un peuplement forestier, caractérisation de structures géologiques karstiques).

Mots-clés : surfaces paramétriques, maillages, objets discrets, analyse de forme, extraction d’information, modélisation par contraintes