Période : 2004 – 2016
Membres impliqués : Alexandra Bac, Jean-Luc Mari, Aldo Gonzalez
Lorenzo.
Collaborations : Département de Mathématiques Appliquées (Université de Séville, Espagne).
Mots-clés : géométrie discrète, topologie discrète, squelettisation, amincissement homotopique, description de formes, morphologie mathématique, complexe cubique, homologie, théorie de l’homologie
effective, théorie discrète de Morse.
Description du projet :
L’homologie s’est révélée comme un très bon outil pour la classification et la compréhension des objets discrets, notamment quand ils ont plus de trois dimensions. Elle fournit une classe de descripteurs qui synthétisent la structure basique de la forme considérée.
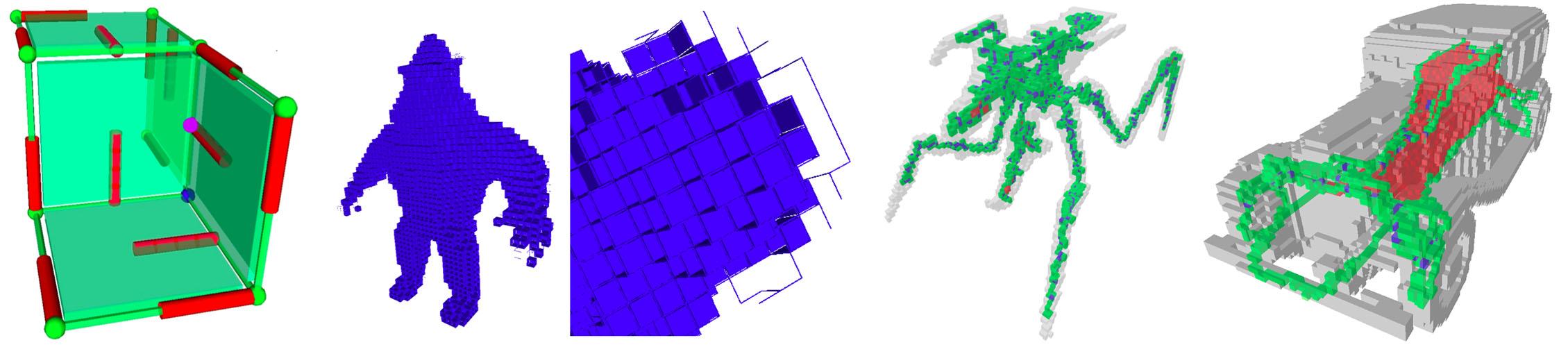
L’homologie formalise la notion de « trou » dans un objet. On peut classifier les « trous » par leur dimension : les 0-trous sont les composantes connexes ; les 1-trous, les tunnels et les 2-trous, les cavités. Le calcul de l’information homologique a pour but, entre autres, de déterminer le nombre de ces trous (nombre de Betti) et un représentant de chacun (cycle représentatif ou générateur d’homologie).
Notre travail s’appuie sur deux approches antérieures : la théorie de l’homologie effective [Ser92] et la théorie discrète de Morse [For02]. Notre principal résultat est une approche combinant ces deux théories, en en conservant les avantages tout en dépassant leurs limitations respectives. Nous avons baptisé « Homological Discrete Vector Field » (HDVF), ces champs de vecteurs gradient discret, généralisant l’outil principal de la théorie discrète de Morse en autori- sant les cycles, ce qui permet de calculer l’homologie exacte (et pas seulement une approximation).
Notre objectif est d’appliquer l’outil homologique des HDVF dans le domaine de la géométrie et de la géométrie discrète : extraction de squelettes, de caractéristiques de porosité (que ce soit en géologie ou en foresterie) …

Commentaires récents