Journée séminaire S. Peltier / G. Morin (21/09/2023)

Pour notre séminaire de reprise, nous avons le plaisir de recevoir pour un double séminaire :

Samuel Peltier

Calcul incrémental des groupes d'homologie d'un objet
  • Date : 21/09/2023 – 10h
  • Salle : Polytech Luminy bât. A – amphi A
  • Zoom : https://univ-amu-fr.zoom.us/j/88082735588?pwd=QlJlZzM1WUNIRGt1ZEdrb0hLMTJhdz09
  • Samuel Peltier, XLIM
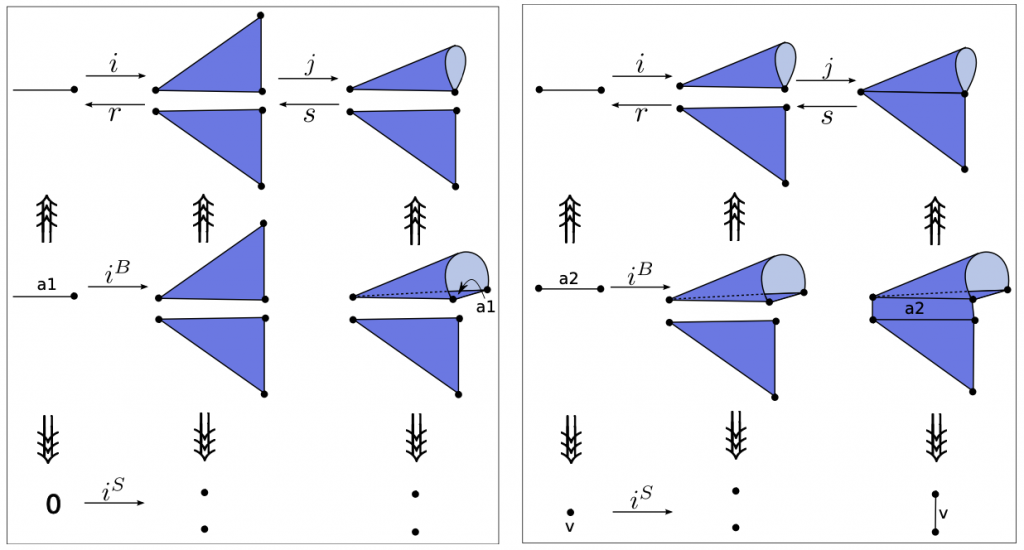
  • Titre : Calcul incrémental de groupes d’homologie
  • Résumé : L’homologie est un invariant topologique classiquement étudié en topologie albébrique.
    Utilisé dans le cadre de la modélisation géométrique à base topologique, l’homologie permet de caractériser les « trous » d’un objet subdivisé (composantes connexes, tunnels, cavités, etc.).
    Une approche classique « globale » consiste à étudier les relations d’incidence de l’ensemble des cellules de l’objet subdivisé. Le calcul incrémental de l’homologie d’un objet subdivisé s’attache à effectuer le calcul étape après étape, par exemple, en analysant la construction de l’objet elle même.
    L’approche est ici « locale » : connaissant l’homologie d’un objet à une étape de sa construction, l’homologie de l’opération effectuée, il est possible d’en déduire l’homologie de l’objet résultant sans avoir à effectuer un calcul global.
    Dans cette présentation, les points suivants seront abordés :
    • rappel de l’ensemble des outils et notions de base de l’homologie effective,
    • mise en application directe pour le suivi de l’homologie d’un objet au cours de sa construction, donnée par une suite d’opérations d’identification,
    • utilisation de l’homologie effective pour le calcul direct de l’homologie de structures cellulaires de type cartes combinatoires.

Géraldine Morin

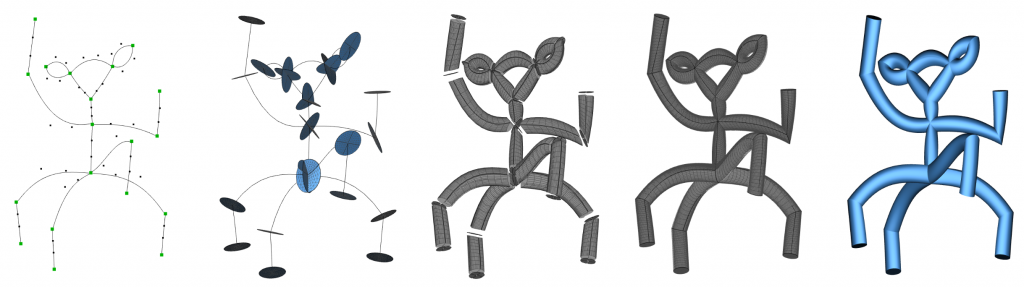
  • Date : 21/09/2023 – 14h30
  • Salle : Polytech Luminy bât. A – amphi A
  • Zoom : https://univ-amu-fr.zoom.us/j/88082735588?pwd=QlJlZzM1WUNIRGt1ZEdrb0hLMTJhdz09
  • Géraldine Morin, IRIT
  • Titre : Modélisation par squelettes en 2D et 3D : génération d’objets à partir de squelette et inversement
  • Résumé : Les représentations par squelette offrent une modélisation d’une forme 2D ou 3D de dimension inférieure : un ensemble de courbes pour les formes 2D, un ensemble de feuillets et de courbes pour les modèles 3D. Nous proposons plusieurs applications se basant sur ces bonnes propriétés des squelettes.
    Nous proposons tout d’abord une méthode de génération de modèles volumiques tubulaires à partir de squelettes curvilignes 3D. La cohérence de la topologie de l’objet volumique est assurée par l’utilisation des ensembles semi-simploïdaux. Les branches sont jointes aux sommets du squelette de façon continue et toute configuration topologique peut être générée. Les ensembles semi-simploïdaux sont réalisés géométriqauement dans des espaces de Bézier.
    Nous proposons ensuite un algorithme d’estimation de squelette 2D et 3D efficace et robuste, qui permet de générer un squelette non bruité qui garantit une epsilon-approximation de la forme originale au sens de la distance de Hausdorff. Ensuite, nous verrons comment l’estimation robuste du squelette 2D peut permettre de proposer la reconstruction d’un objet tubulaire composé de branches.
    Collaboration : G. Morin, S. Peltier, Kathryn Leonard, Occidental College, U.S.A.